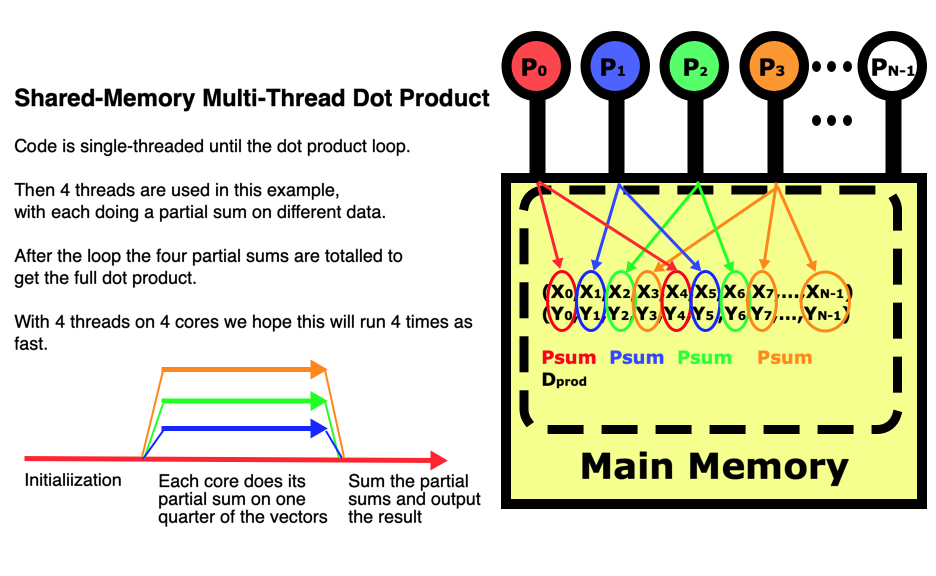
Let’s go through the multi-threaded version of the dot product code
below to illustrate the changes that had to be made to the code to
parallelize it. The pymp package needs to be installed
into our virtual environment by doing pip install
pymp-pypi. Once that is installed, the import
pymp line will bring those functions into the code.
When we run the code we will want to set the number of threads for it
to use. In the code below, this is being set internally using the number
of threads passed in as a command line argument. This is used to set the
number of threads using the pymp.config.num_threads
variable. The other method of setting the number of threads is to use
the environmental variable PYMP_NUM_THREADS externally.
For example, in your job script you can have a line export
PYMP_NUM_THREADS=4 to tell the program to use 4 threads.
Right before the loop we must define our parallel environment with
the line with pymp.Parallel( nthreads ) as p: which
spins up the threads with the fork method. Then the for loop range is
changed so that each thread has a different range for the elements of
the loop that each thread is responsible for.
In the OpenMP multi-threading package used with C/C++ and Fortran,
you can use the same variable d_prod in the loop and just declare it as
a variable to be used locally within each thread then globally summed at
the end, which is called a reduction. This is very
convenient and requires fewer changes to the code, but the
pymp package does not support this added function by
choice opting for the Python way of doing it more explicitly, so in our
code we need to create a shared array of partial sums and manually sum
them together at the end. This is just as efficient computationally, it
just takes a little extra coding but is more explicit.
PYTHON
# Do the dot product between two vectors X and Y then print the result
# USAGE: python dot_product_threaded.py 4 to run on 4 threads
import sys
import time
import pymp
# Get and set nthreads from the command line
pymp.config.num_threads = int( sys.argv[1] )
nthreads = pymp.config.num_threads
N = 100000000 # Do a large enough test to reduce timing variance
x = [ float( i ) for i in range( N ) ]
y = [ float( i ) for i in range( N ) ]
# Now initialize a very large dummy array to force X and Y out of all levels of cache
# so that our times are for pulling elements up from main memory.
dummy = [ 0.0 for i in range( 125000000 ) ] # Initialize 1 GB of memory
# Now we start our timer and do our calculation using multiple threads
t_start = time.perf_counter()
psum = pymp.shared.array( (nthreads,), dtype='float' )
for i in range( nthreads ):
psum[i] = 0.0
d_prod = 0.0
with pymp.Parallel( nthreads ) as p:
for i in p.range( N ):
#d_prod += x[i] * y[i]
psum[p.thread_num] += x[i] * y[i]
for i in range( nthreads ): # Explicitly do the reduction across threads
d_prod += psum[i]
t_elapsed = time.perf_counter() - t_start
# The calculation is done and timer stopped so print out the answer
print('dot product = ', d_prod, 'took ', t_elapsed, ' seconds' );
print( 2.0*N*1.0e-9 / t_elapsed, ' Gflops (billion floating-point operations per second)')
print( 2.0*N*8.0/1.0e9, ' GB memory used' )
Let’s go through the multi-threaded version of the dot product code
below to illustrate the changes that had to be made to the code to
parallelize it. In R we need to define a virtual cluster that will be
used to spread the work from the for loops across the
CPU cores. This can be done in several ways in R and the choice should
come down to what works best for the problem you are coding up.
We start by loading the library parallel in the
first example code below to pull in the detectCores(), makeCluster(),
clusterExport(), and clusterApply() functions. We next detect the number
of cores accessible to the job then define the cluster with
makeCluster() spawning independent worker processes to
handle parts of the parallel processing. For this
parallel library we need the body of the loop to be put
into a function and any variables that need to be used inside this
function must be exported using clusterExport()
commands. The clusterApply() command uses the cluster
object, iteration range, and function name which then spawns multiple
processes to execute the function for the iteration loop, automatically
splitting them across the cores in the virtual cluster on a single
compute node. At the end there is a stopCluster()
statement that cleans up the virtual cluster before the program
ends.
This basic approach is simple and can be useful but also may be
inefficient since the overhead for dividing the work between threads may
be much greater than the work done within each iteration, as is clearly
the case in our simple example where there is only a single
multiplication for each pass through the loop. In the second part of
this code, the loop is instead divided over the number of threads with
the function then manually splitting the loop iterations internally.
This greatly limits the assignment-of-work overhead since only the
initial assignment is needed and you will see for yourself that the
resulting performance is enormously better.
R
# Dot product in R using a loop and a vector summation
# USAGE: Rscript dot_product_multi_thread.R 100000 8 for 100,000 elements on 8 cores
library( parallel )
# Get the vector size and nThreads from the command line
args <- commandArgs(TRUE)
if( length( args ) == 2 ) {
n <- as.integer( args[1] )
nThreads <- as.integer( args[2] )
} else {
n <- 100000
nThreads <- detectCores()
}
cl <- makeCluster( nThreads )
# Allocate space for and initialize the arrays
x <- vector( "double", n )
y <- vector( "double", n )
for( i in 1:n )
{
x[i] <- as.double(i)
y[i] <- as.double(3*i)
}
# Export variables needed within the functions
clusterExport( cl, "x" )
clusterExport( cl, "y" )
clusterExport( cl, "n" )
clusterExport( cl, "nThreads" )
# Time a multi-threaded dot product even though it's inefficient
dot_product_function <- function( i ) {
return( x[i] * y[i] )
}
dummy <- matrix( 1:125000000 ) # Clear the cache buffers before timing
t_start <- proc.time()[[3]]
dot_product_list <- clusterApply( cl, 1:n, dot_product_function )
dot_product <- sum( unlist(dot_product_list) )
t_end <- proc.time()[[3]]
print(sprintf("Threaded dot product by clusterApply took %6.3f seconds", t_end-t_start))
print(sprintf("dot_product = %.6e on %i threads for vector size %i", dot_product, nThreads, n ) )
# Now try dividing the iterations manually between workers
dot_product_workers <- function( myThread ) {
mySum <- 0.0
for( i in seq( myThread, n, by = nThreads ) )
{
mySum <- mySum + x[i] * y[i]
}
return( mySum )
}
dummy <- matrix( 1:125000000 ) # Clear the cache buffers before timing
t_start <- proc.time()[[3]]
dot_product_list <- clusterApply( cl, 1:nThreads, dot_product_workers )
dot_product <- sum( unlist(dot_product_list) )
t_end <- proc.time()[[3]]
print(sprintf("Threaded dot product with nThreads workers took %6.3f seconds", t_end-t_start))
print(sprintf("dot_product = %.6e on %i threads for vector size %i", dot_product, nThreads, n ) )
stopCluster( cl )
This second multi-threaded example below uses the
foreach and doParallel libraries. This
code similarly defines and initiates a virtual cluster. The
foreach loop is similar to a for loop
but you can choose between different back ends. A %do%
back end would run the body in scalar, while the %dopar
will split the iterations across the cores of the virtual cluster, and
we will discuss later that there is a %doMPI% back end
that can split the work across cores on different compute nodes. While
similar to the previous example, the foreach approach
is cleaner programming in that you don’t have to create a separate
function for the body of the loop. You also don’t need to manually
export variables since the processes that are spawned inherit the
environment of the parent process. So we get more flexibility in the
back ends as well as a more convenient programming approach. You’ll be
asked to measure the performance of each approach in the exercise
below.
R
# Dot product in R using a loop and a vector summation
# USAGE: Rscript dot_product_threaded_dopar.R 100000 8 for 100,000 elements on 8 threads
library( foreach )
library( iterators )
library( parallel )
library( doParallel )
# Get the vector size and nThreads from the command line
args <- commandArgs(TRUE)
if( length( args ) == 2 ) {
n <- as.integer( args[1] )
nThreads <- as.integer( args[2] )
} else {
n <- 100000
nThreads <- detectCores()
}
# Initialize the vectors and our virtual cluster
x <- vector( "double", n )
y <- vector( "double", n )
for( i in 1:n )
{
x[i] <- as.double(i)
y[i] <- as.double(3*i)
}
cl <- makeCluster( nThreads )
registerDoParallel( cl, nThreads )
# Time the multi-threaded dot product foreach loop
# This returns a vector of size 'n' that will need to be summed
# so it is very inefficient.
dummy <- matrix( 1:125000000 ) # Clear the cache buffers before timing
t_start <- proc.time()[[3]]
#dot_product_vector <- foreach( i = 1:n, .combine = c, mc.preschedule = TRUE ) %dopar% {
dot_product_vector <- foreach( i = 1:n, .combine = c ) %dopar% {
x[i] * y[i]
}
dot_product <- sum( dot_product_vector )
t_end <- proc.time()[[3]]
print(sprintf("dopar dot product took %6.3f seconds", t_end-t_start))
print(sprintf("dot_product = %.6e on %i threads for vector size %i", dot_product, nThreads, n ) )
# Now let's try a more complex but more efficient method where
# we manually divide the work between the threads.
dummy <- matrix( 1:125000000 ) # Clear the cache buffers before timing
t_start <- proc.time()[[3]]
dot_product_vector <- foreach( myThread = 1:nThreads, .combine = c ) %dopar% {
psum <- 0.0
for( j in seq( myThread, n, nThreads ) ) {
psum <- psum + x[j] * y[j]
}
psum
}
dot_product <- sum( dot_product_vector )
t_end <- proc.time()[[3]]
print(sprintf("dopar dot product with nThreads workers took %6.3f seconds", t_end-t_start))
print(sprintf("dot_product = %.6e on %i threads for vector size %i", dot_product, nThreads, n ) )
stopCluster( cl )
Let’s go through the multi-threaded version of the dot product code
below to illustrate the changes that had to be made to the code to
parallelize it. In C/C++ we need a line #include
<omp.h> to bring the OpenMP headers, then the code needs
to be compiled with the -fopenmp flag for
gcc or the -qopenmp flag for
icc.
When we run the code we will want to set the number of threads for it
to use. In the code below, this is being set internally using the number
of threads passed in as a command line argument. This is used to set the
number of threads using the omp_set_num_threads()
function in C/C++. The other method of setting the number of threads is
to use the environmental variable OMP_NUM_THREADS for
C/C++/Fortran. For example, in your job script you can have a line
export OMP_NUM_THREADS=4 to tell the program to use 4
threads.
Right before the loop we must tell the compiler to parallelize the
loop using a #pragma omp parallel for statement, plus
we need to indicate that there is a summation reduction of
dprod taking place where the partial sums calculated by
each thread get globally summed at the end. Then the for loop range is
changed so that each thread has a different range for the elements of
the loop that each thread is responsible for.
C
// Dot product in C using OpenMP
// USAGE: dot_product_openmp 4 to run with 4 cores
#include <stdio.h>
#include <stdlib.h>
#include <time.h>
#include <sys/time.h>
#include <omp.h>
void main (int argc, char **argv)
{
int i, N;
double dprod, *X, *Y;
double t_elapsed;
struct timespec ts, tf;
// Get the number of threads from the command line
char *a = argv[1];
int nthreads = atoi( a );
N = 100000000;
// Allocate space for the X and Y vectors
X = malloc( N * sizeof(double) );
Y = malloc( N * sizeof(double) );
// Initialize the X and Y vectors
for( i = 0; i < N; i++ ) {
X[i] = (double) i;
Y[i] = (double) i;
}
// Allocate and innitialize a dummy array to clear cache
double *dummy = malloc( 125000000 * sizeof(double) );
for( i = 0; i < 125000000; i++ ) { dummy[i] = 0.0; }
// Now we start the timer and do our calculation
clock_gettime(CLOCK_REALTIME, &ts);
omp_set_num_threads( nthreads );
dprod = 0.0;
#pragma omp parallel for reduction( +:dprod)
for( i = 0; i < N; i++ ) {
dprod += X[i] * Y[i];
}
clock_gettime(CLOCK_REALTIME, &tf);
t_elapsed = (double) ( tf.tv_sec - ts.tv_sec );
t_elapsed += (double) (tf.tv_nsec - ts.tv_nsec) * 1e-9;
printf("dot product = %e on %d threads took %lf seconds\n", dprod, nthreads, t_elapsed );
printf("%lf Gflops (billion floating-point operations per second)\n",
2.0*N*1.0e-9 / t_elapsed);
printf( "%lf GB memory used\n", 2.0*N*8.0/1.0e9);
}
Let’s go through the multi-threaded version of the dot product code
below to illustrate the changes that had to be made to the code to
parallelize it. In Fortran we need a line USE omp_lib
to bring the OpenMP functions, then the code needs to be compiled with
the -fopenmp flag for gfortran or the
-qopenmp flag for ifort.
When we run the code we will want to set the number of threads for it
to use. In the code below, this is being set internally using the number
of threads passed in as a command line argument. This is used to set the
number of threads using the OMP_SET_NUM_THREADS()
subroutine in Fortran. The other method of setting the number of threads
is to use the environmental variable OMP_NUM_THREADS
for C/C++/Fortran. For example, in your job script you can have a line
export OMP_NUM_THREADS=4 to tell the program to use 4
threads.
Right before the loop we must tell the compiler to parallelize the
loop using a !$OMP PARALLEL DO statement, plus we need
to indicate that there is a summation reduction of
dprod taking place where the partial sums calculated by
each thread get globally summed at the end. Then the DO
loop range is changed so that each thread has a different range for the
elements of the loop that each thread is responsible for.
FORTRAN
! Dot product in Fortran using OpenMP
PROGRAM dot_product_fortran_openmp
USE omp_lib
INTEGER :: i, n, nthreads
CHARACTER(100) :: arg1
DOUBLE PRECISION :: dprod, t_start, t_elapsed
DOUBLE PRECISION, ALLOCATABLE :: x(:), y(:)
DOUBLE PRECISION, ALLOCATABLE :: dummy(:)
! Dynamically allocate large arrays to avoid overflowing the stack
n = 100000000
ALLOCATE( x(n) )
ALLOCATE( y(n) )
ALLOCATE( dummy(125000000) )
! Set the number of threads from the command line argument
CALL GET_COMMAND_ARGUMENT( 1, arg1 )
READ( arg1, *) nthreads
CALL OMP_SET_NUM_THREADS( nthreads ) ! Set the number of threads
! Initialize the vectors
DO i = 1, n
x(i) = i
y(i) = i
END DO
! Initialize a dummy array to clear cache
DO i = 1, 125000000
dummy(i) = 0.0
END DO
! Now start the timer and do the calculations
t_start = OMP_GET_WTIME()
dprod = 0.0
!$OMP PARALLEL DO REDUCTION(+:dprod)
DO i = 1, n
dprod = dprod + x(i) * y(i)
END DO
t_elapsed = OMP_GET_WTIME() - t_start
WRITE(*,*) "dot product = ", dprod, " took ", &
t_elapsed, " seconds on ", nthreads, " threads"
END PROGRAM dot_product_fortran_openmp